1계논리의 추론규칙

아래의 추론규칙들에서 쓰인 φ(x)라는 표현은 x가 φ의 자유변수로 꼭 나타나야 한다는 것을 의미하는 것이 아니며 또한 φ가 x 이외의 다른 자유변수를 가질 수 없다는 것을 의미하는 것도 아니다. 논리식 φ를 φ(x)로 나타내는 표현법은 단지 φ에서 x의 모든 자유나타남을 t로 대체하여 얻은 논리식을 φ(t)로 나타내기 위한 것이다. 만일 φ에 x의 자유나타남이 없다면 φ(t)는 φ(x)와 동일한 논리식이 된다.

	도입	소거
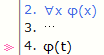
∀	c는 새로운 상수기호, x는 새로운 자유변수 ∀x φ(x) 대신 ∀y φ(y)를 써도 됨	t는 φ안에서 x를 치환가능
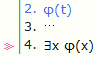
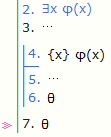
∃	t는 φ안에서 x를 치환가능	c는 새로운 상수기호이고 θ에 나타나지 않음 x는 새로운 자유변수이고 θ의 자유변수가 아님
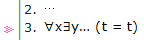
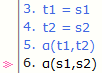
=	t는 임의의 논리항	논리항 t1,t2,s1,s2의 어떤 변수도 논리식 α에서 묶여 나타날 수 없음
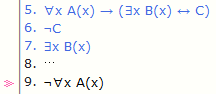
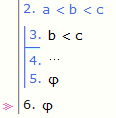
명논귀결	결론은 전제들의 명제논리적 귀결. 오른쪽 예에서 보듯이 전제로 부분증명을 사용할 수도 있음.
확장 버전
	도입	소거
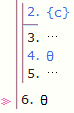
∀	c1,c2 대신 x1,x2 사용 가능 ∀x1∀x2 대신 ∀x2∀x1 사용 가능
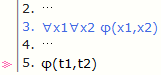
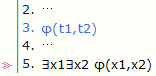
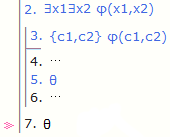
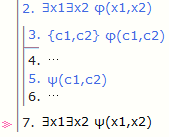
∃		c1,c2 대신 x1,x2(혹은 y1,y2) 사용 가능 ∃x1∃x2 대신 ∃x2∃x1 사용 가능
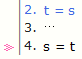
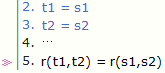
= 소거	Symmetricity   = elim for identity   Transitivity
∀= 소거	[= 소거]의 전제로 등식 t(x1,x2)=s(x1,x2) 대신 항등식 ∀x1∀x2(t(x1,x2)=s(x1,x2))를 사용할 수 있다. 이 경우 Proofmood는 적당한 논리항 r1,r2에 대하여 전제 t(r1,r2)=s(r1,r2)가 있는 것처럼 처리한다. 다만 Transitivity의 경우 여러 개의 전제 중 가장 마지막 전제 하나에만 이러한 항등식을 사용할 수 있다.
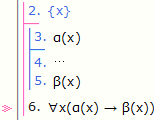
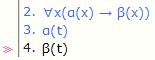
∀→	{c} 대신 {c1,c2} 등을 쓸 수 있다. 별도의 메뉴 없이 그냥 [∀ 도입]을 사용한다.	∀x 대신 ∀x1∀x2 등을 쓸 수 있다. 별도의 메뉴 없이 그냥 [∀ 소거]를 사용한다.
결합법칙	결합법칙 ∀x∀y∀z(x·y·z = x·(y·z))과 [= 소거]를 여러 번 반복 적용하여 얻을 수 있는 등식, 예를 들어 a·(b·c)·(d·e) = a·(b·(c·d))·e를 이 규칙을 단 한 번 사용하여 얻을 수 있다. 물론 결합법칙 ∀x∀y∀z(x·y·z = x·(y·z))는 전제로 지정되어 있어야 한다.
1논공식	단, dummy, antecedent, consequent 관련 6개의 공식에서는 β에 x가 자유변수로 나타나지 않는다.
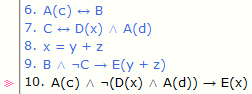
동등대체	결론(10번 라인)은 마지막 전제(9번 라인)에서 적절히 선택한 논리항 및 부분논리식들을, 이전의 전제들(6,7,8번 라인)에서 지정된 동등한 논리항 및 부분논리식들로 대체하여 얻음. 치환에 있어서의 자유 나타남 보존 조건은 만족되어야 함.
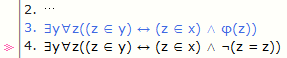
메타치환	메타술어기호를 사용한 논리식 φ(z)를 다른 논리식으로 치환함. 단, 치환하는 논리식 (¬(z=z))의 자유변수 중에 φ에 나타나지 않는 것은 새 논리식 (라인 4) 안에서 자유로이 나타나야 함.

[Fitch, 1st-order]